注册登录

7.4 Verilog CIC 滤波器设计

积分梳状滤波器（CIC，Cascaded Integrator Comb），一般用于数字下变频（DDC）和数字上变频（DUC）系统。CIC 滤波器结构简单，没有乘法器，只有加法器、积分器和寄存器，资源消耗少，运算速率高，可实现高速滤波，常用在输入采样率最高的第一级，在多速率信号处理系统中具有着广泛应用。

DDC 原理

DDC 工作原理

DDC 主要由本地振荡器（NCO） 、混频器、滤波器等组成，如下图所示。

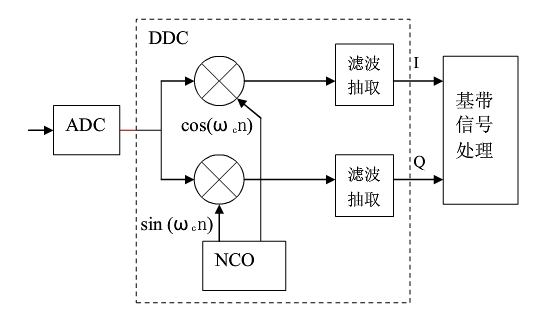
20211122192152860029500

DDC 将中频信号与振荡器产生的载波信号进行混频，信号中心频率被搬移，再经过抽取滤波，恢复原始信号，实现了下变频功能。

中频数据采样时，需要很高的采样频率来确保 ADC（模数转换器）采集到信号的信噪比。经过数字下变频后，得到的基带信号采样频率仍然是 ADC 采样频率，所以数据率很高。此时基带信号的有效带宽往往已经远小于采样频率，所以利用抽取、滤波进行数据速率的转换，使采样率降低，避免资源的浪费和设计的困难，就成为 DDC 不可缺少的一部分。

而采用 CIC 滤波器进行数据处理，是 DDC 抽取滤波部分最常用的方法。

带通采样定理

在 DDC 系统中，输入的中频载波信号会根据载波频率进行频移，得到一个带通信号。如果此时仍然采用奈奎斯特采样定理，即采样频率为带通信号最高频率的两倍，那么此时所需的采样频率将会很高，设计会变的复杂。此时可按照带通采样定理来确定抽样频率。

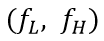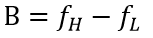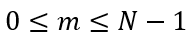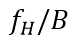带通采样定理：一个频带限制在20211122192153717259301的连续带通信号，带宽为20211122192153174451002。令20211122192154631722603 ，其中 N 为不大于 20211122192154488661904的最大正整数，如果采样频率满足条件：

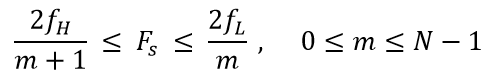
20211122192155745683905

则该信号完全可以由其采样值无失真的重建。

当 m=1 时，带通采样定理便是奈奎斯特采样定理。

带通采样定理的另一种描述方式为：若信号最高频率为信号带宽的整数倍，采样频率只需大于信号带宽的两倍即可，此时不会发生频谱混叠。

所以，可以认为采样频率的一半是 CIC 滤波器的截止频率。

DDC 频谱搬移

例如一个带宽信号中心频率为 60MHz，带宽为 8MHz, 则频率范围为 56MHz ~ 64MHz，m 的可取值范围为 0 ~ 7。取 m=1, 则采样频率范围为 64MHz ~ 112MHz。

取采样频率为 80MHz，设 NCO 中心频率为 20 MHz，下面讨论复信号频谱搬移示意图。

（1）考虑频谱的对称性，输入复信号的频谱示意图如下：

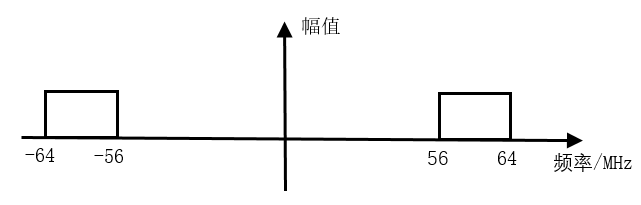
20211122192156203984806

（2）80MHz 采样频率采样后，56~64MHz 的频带被搬移到了 -24~ -16MHz 与 136 ~ 144MHz（高于采样频率被滤除）的频带处，-64~ -56MHz 的频带被搬移到 -144~ -136MHz（高于采样频率被滤除）与 16~24MHz 的频带处。

采样后频带分布如下：

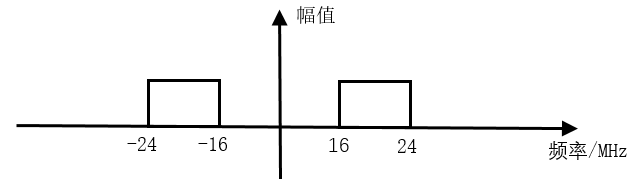
20211122192156660210307

（3）信号经过 20MHz NCO 的正交电路后， -24~ -16MHz 的频带被搬移到 -4~4MHz 与 -44~ -36MHz 的频带处，16~24MHz 的频带被搬移到 -4~4MHz 与 36~44MHz 的频带处，如下所示。

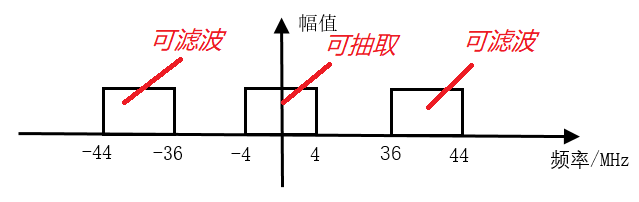
20211122192157118567708

（4）此时中频输入的信号已经被搬移到零中频基带处。

-44~ -36MHz 和 36~44MHz 的带宽信号是不需要的，可以滤除；-4~4MHz 的零中频信号数据速率仍然是 80MHz，可以进行抽取降低数据速率。而 CIC 滤波，就是要完成这个过程。

上述复习了很多数字信号处理的内容，权当抛 DDC 的砖，引 CIC 的玉。

CIC 滤波器原理

单级 CIC 滤波器

设滤波器抽取倍数为 D，则单级滤波器的冲激响应为：

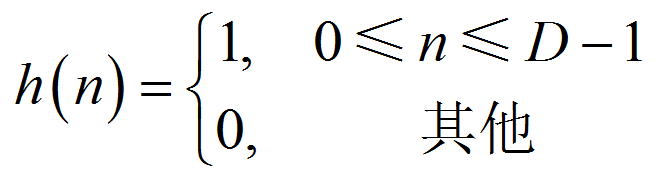
20211122192157875448709

对其进行 z 变换，可得单级 CIC 滤波器的系统函数为：

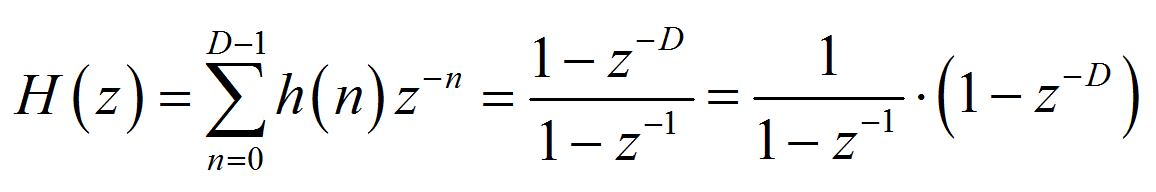
20211122192158832390310

令

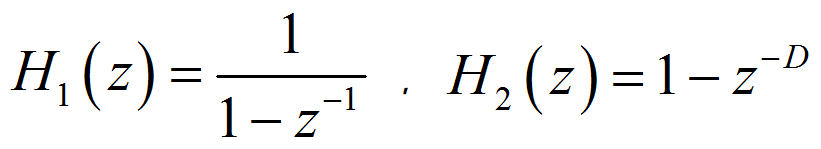
20211122192158589251611

可以看出，单级 CIC 滤波器包括两个基本组成部分：积分部分和梳状部分，结构图如下：

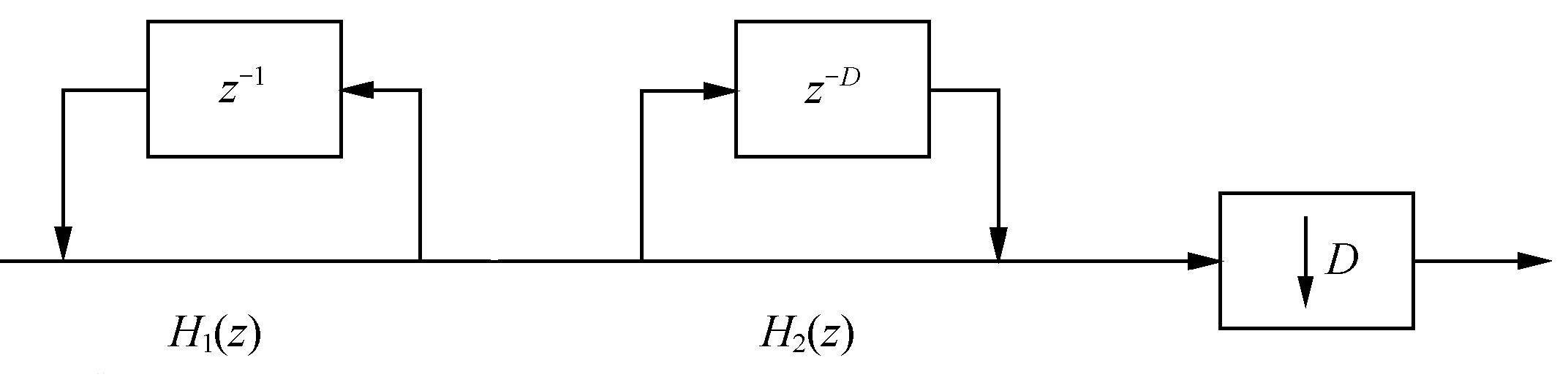
20211122192159747977712

积分器

积分器是一个单级点的 IIR（Infinite Impulse Response，无限长脉冲冲激响应）滤波器，且反馈系数为 1，其状态方程和系统函数分别为：

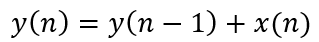
20211122192200509704813

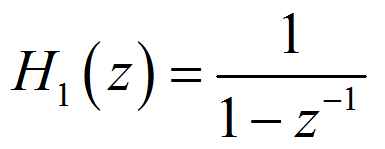
20211122192200368687414

梳状器

梳状器是一个 FIR 滤波器，其状态方程和系统函数分别为：

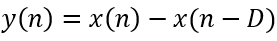
20211122192201427858415

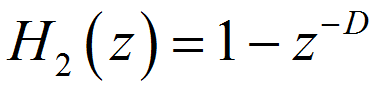
20211122192201684163616

抽取器

在积分器之后，还有一个抽取器，抽取倍数与梳状器的延时参数是一致的。利用 z 变换的性质进行恒等变换，将抽取器移动到积分器与梳状器之间，可得到单级 CIC 滤波器结构，如下所示。

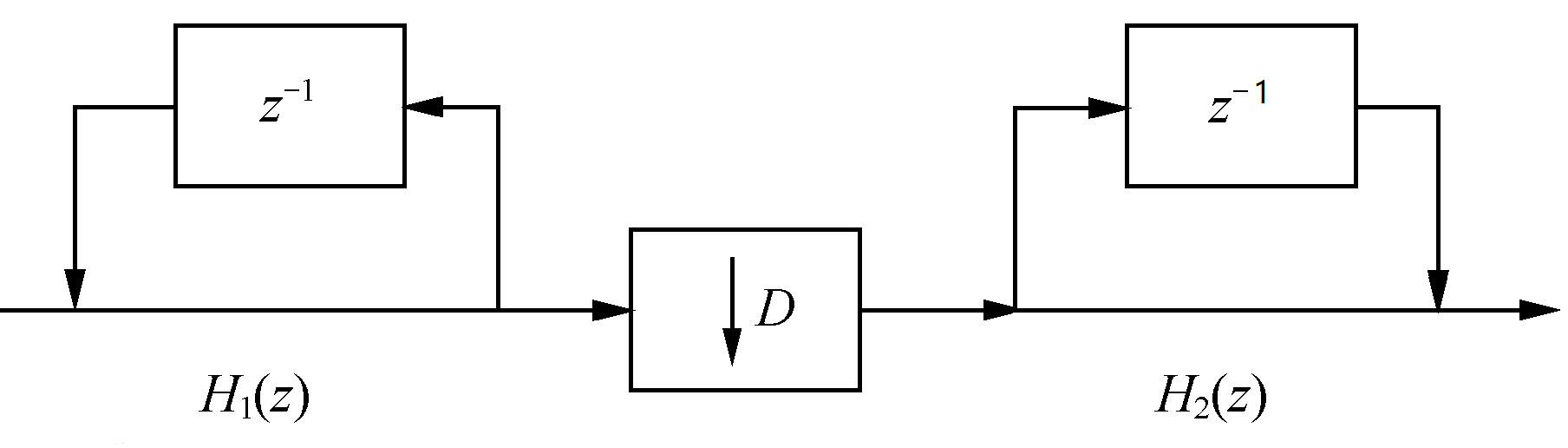
20211122192202243042017

参数说明

CIC 滤波器结构变换之前的参数 D 可以理解为梳状滤波器的延时或阶数；变换之后，D 的含义 变为抽取倍数，而此时梳状滤波器的延时为 1，即阶数为 1。

很多学者会引入一个变量 M，表示梳状器每一级的延时，此时梳妆部分的延时就不为 1 了。那么梳状器的系统函数就变为：

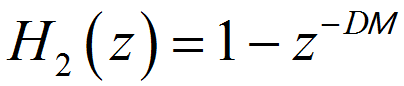
20211122192203248640618

其实把 DM 整体理解为单级滤波器延时，或者抽取倍数，也都是可以的。可能实现的方式或结构不同，但是最后的结果都是一样的。本次设计中，单级滤波器延时都为 M=1，即抽取倍数与滤波延时相同。

多级 CIC 滤波器

单级 CIC 滤波器的阻带衰减较差，为了提高滤波效果，抽取滤波时往往会采用多级 CIC 滤波器级联的结构。

实现多级直接级联的 CIC 滤波器在设计和资源上并不是最优的方式，需要对其结构进行调整。如下所示，将积分器和梳状滤波器分别移至一组，并将抽取器移到梳状滤波器之前。先抽取再进行滤波，可以减少数据处理的长度，节约硬件资源。

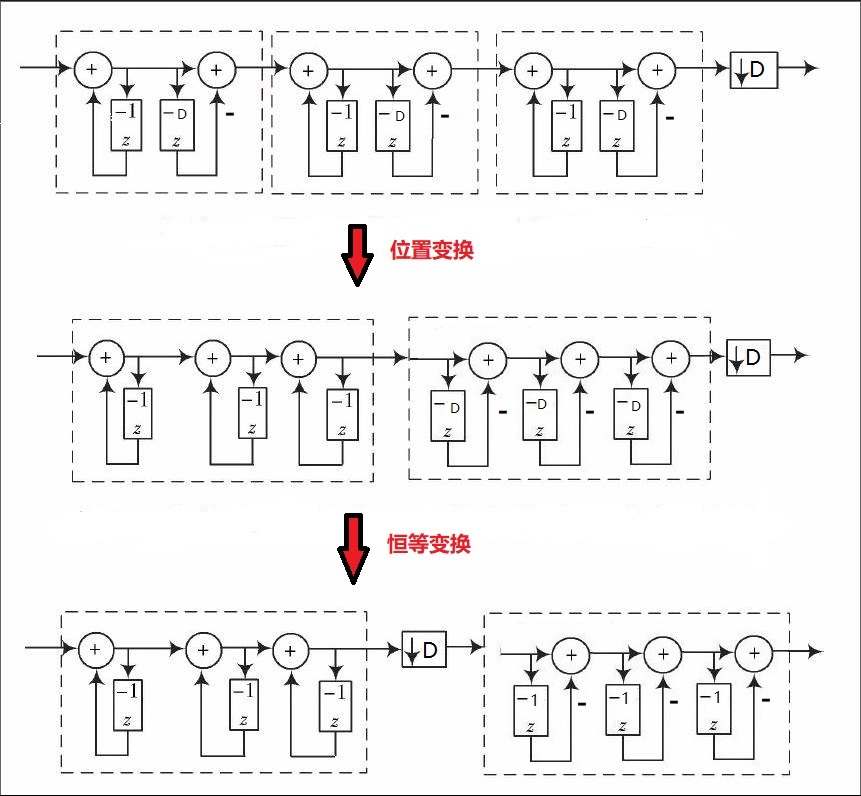
20211122192204412706119

当然，级联数越大，旁瓣抑制越好，但是通带内的平坦度也会变差。所以级联数不宜过多，一般最多 5 级。

CIC 滤波器设计

设计说明

CIC 滤波器本质上就是一个简单的低通滤波器，截止频率为采样频率除以抽取倍数后的一半。输入数据信号仍然是 7.5MHz 和 250KHz，采样频率 50MHz。抽取倍数设置为 5，则截止频率为 5MHz，小于 7.5MHz，可以滤除 7.5MHz 的频率成分。设计参数如下：

输入频率：    7.5MHz 和 250KHz
采样频率：    50MHz
阻带：           5MHz 
阶数：           1（M=1）
级数：           3（N=3）

关于积分时中间数据信号的位宽，很多地方给出了不同的计算方式，计算结果也大相径庭。这里总结一下使用最多的计算方式：

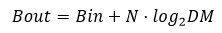
20211122192204772291820

其中，D 为抽取倍数，M 为滤波器阶数，N 为滤波器级数。抽取倍数为 5，滤波器阶数为 1，滤波器级联数为 3，取输入信号数据位宽为 12bit，对数部分向上取整，则积分后数据不溢出的中间信号位宽为 21bit。

为了更加宽裕的设计，滤波器阶数如果理解为未变换结构前的多级 CIC 滤波器直接型结构，则滤波器阶数可以认为是 5，此时中间信号最大位宽为 27bit。

积分器设计

根据输入数据的有效信号的控制，积分器做一个简单的累加即可，注意数据位宽。

实例


//3 stages integrator

module integrator

    #(parameter NIN     = 12,

      parameter NOUT    = 21)

    (

      input               clk ,

      input               rstn ,

      input               en ,

      input [NIN-1:0]     din ,

      output              valid ,

      output [NOUT-1:0]   dout) ;



    reg [NOUT-1:0]         int_d0  ;

    reg [NOUT-1:0]         int_d1  ;

    reg [NOUT-1:0]         int_d2  ;

    wire [NOUT-1:0]        sxtx = {{(NOUT-NIN){1'b0}}, din} ;



    //data input enable delay

    reg [2:0]              en_r ;

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            en_r   <= 'b0 ;

        end

        else begin

            en_r   <= {en_r[1:0], en};

        end

    end



    //integrator

    //stage1

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            int_d0        <= 'b0 ;

        end

        else if (en) begin

            int_d0        <= int_d0 + sxtx ;

        end

    end



    //stage2

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            int_d1        <= 'b0 ;

        end

        else if (en_r[0]) begin

            int_d1        <= int_d1 + int_d0 ;

        end

    end



   //stage3

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            int_d2        <= 'b0 ;

        end

        else if (en_r[1]) begin

            int_d2        <= int_d2 + int_d1 ;

        end

    end

    assign dout  = int_d2 ;

    assign valid = en_r[2];



endmodule

抽取器设计

抽取器设计时，对积分器输出的数据进行计数，然后间隔 5 个数据进行抽取即可。

实例


module  decimation

    #(parameter NDEC = 21)

    (

     input                clk,

     input                rstn,

     input                en,

     input [NDEC-1:0]     din,

     output               valid,

     output [NDEC-1:0]    dout);



    reg                  valid_r ;

    reg [2:0]            cnt ;

    reg [NDEC-1:0]       dout_r ;



    //counter

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            cnt <= 3'b0;

        end

        else if (en) begin

            if (cnt==4) begin

                cnt <= 'b0 ;

            end

            else begin

                cnt <= cnt + 1'b1 ;

            end

        end

    end



    //data, valid

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            valid_r        <= 1'b0 ;

            dout_r         <= 'b0 ;

        end

        else if (en) begin

            if (cnt==4) begin

                valid_r     <= 1'b1 ;

                dout_r      <= din;

            end

            else begin

                valid_r     <= 1'b0 ;

            end

        end

    end

    assign dout          = dout_r ;

    assign valid         = valid_r ;



endmodule

梳状器设计

梳状滤波器就是简单的一阶 FIR 滤波器，每一级的 FIR 滤波器对数据进行一个时钟延时，然后做相减即可。因为系数为 ±1，所以不需要乘法器。

实例


module comb

    #(parameter NIN  = 21,

      parameter NOUT = 17)

    (

     input               clk,

     input               rstn,

     input               en,

     input [NIN-1:0]     din,

     input               valid,

     output [NOUT-1:0]   dout);



    //en delay

    reg [5:0]                 en_r ;

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            en_r <= 'b0 ;

        end

        else if (en) begin

            en_r <= {en_r[5:0], en} ;

        end

    end

 

    reg [NOUT-1:0]            d1, d1_d, d2, d2_d, d3, d3_d ;

    //stage 1, as fir filter, shift and add(sub), 

    //no need for multiplier

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d1     <= 'b0 ;

        else if (en)      d1     <= din ;

    end

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d1_d   <= 'b0 ;

        else if (en)      d1_d   <= d1 ;

    end

    wire [NOUT-1:0]      s1_out = d1 - d1_d ;



    //stage 2

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d2     <= 'b0 ;

        else if (en)      d2     <= s1_out ;

    end

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d2_d   <= 'b0 ;

        else if (en)      d2_d   <= d2 ;

    end

    wire [NOUT-1:0]      s2_out = d2 - d2_d ;



    //stage 3

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d3     <= 'b0 ;

        else if (en)      d3     <= s2_out ;

    end

    always @(posedge clk or negedge rstn) begin

        if (!rstn)        d3_d   <= 'b0 ;

        else if (en)      d3_d   <= d3 ;

    end

    wire [NOUT-1:0]      s3_out = d3 - d3_d ;



    //tap the output data for better display

    reg [NOUT-1:0]       dout_r ;

    reg                  valid_r ;

    always @(posedge clk or negedge rstn) begin

        if (!rstn) begin

            dout_r         <= 'b0 ;

            valid_r        <= 'b0 ;

        end

        else if (en) begin

            dout_r         <= s3_out ;

            valid_r        <= 1'b1 ;

        end

        else begin

            valid_r        <= 1'b0 ;

        end

    end

    assign       dout    = dout_r ;

    assign       valid   = valid_r ;



endmodule

顶层例化

按信号的流向将积分器、抽取器、梳状器分别例化，即可组成最后的 CIC 滤波器模块。

梳状滤波器的最终输出位宽一般会比输入信号小一些，这里取 17bit。当然输出位宽完全可以与输入数据的位宽一致。

实例


module cic

    #(parameter NIN  = 12,

      parameter NMAX = 21,

      parameter NOUT = 17)

    (

     input               clk,

     input               rstn,

     input               en,

     input [NIN-1:0]     din,

     input               valid,

     output [NOUT-1:0]   dout);



    wire [NMAX-1:0]      itg_out ;

    wire [NMAX-1:0]      dec_out ;

    wire [1:0]           en_r ;



    integrator   #(.NIN(NIN), .NOUT(NMAX))

    u_integrator (

       .clk         (clk),

       .rstn        (rstn),

       .en          (en),

       .din         (din),

       .valid       (en_r[0]),

       .dout        (itg_out));



    decimation   #(.NDEC(NMAX))

    u_decimator (

       .clk         (clk),

       .rstn        (rstn),

       .en          (en_r[0]),

       .din         (itg_out),

       .dout        (dec_out),

       .valid       (en_r[1]));



    comb         #(.NIN(NMAX), .NOUT(NOUT))

    u_comb (

       .clk         (clk),

       .rstn        (rstn),

       .en          (en_r[1]),

       .din         (dec_out),

       .valid       (valid),

       .dout        (dout));



endmodule

testbench

testbench 编写如下，主要功能就是不间断连续的输入 250KHz 与 7.5MHz 的正弦波混合信号数据。输入的混合信号数据也可由 matlab 生成，具体过程参考《并行 FIR 滤波器设计》一节。

实例


module test ;

    parameter    NIN  = 12 ;

    parameter    NMAX = 21 ;

    parameter    NOUT = NMAX ;



    reg                  clk ;

    reg                  rstn ;

    reg                  en ;

    reg  [NIN-1:0]       din ;

    wire                 valid ;

    wire [NOUT-1:0]      dout ;



    //=====================================

    // 50MHz clk generating

    localparam   T50M_HALF    = 10000;

    initial begin

        clk = 1'b0 ;

        forever begin

            # T50M_HALF clk = ~clk ;

        end

    end



    //============================

    //  reset and finish

    initial begin

        rstn = 1'b0 ;

        # 30 ;

        rstn = 1'b1 ;

        # (T50M_HALF * 2 * 2000) ;

        $finish ;

    end



    //=======================================

    // read cos data into register

    parameter    SIN_DATA_NUM = 200 ;

    reg          [NIN-1:0] stimulus [0: SIN_DATA_NUM-1] ;

    integer      i ;

    initial begin

        $readmemh("../tb/cosx0p25m7p5m12bit.txt", stimulus) ;

        i         = 0 ;

        en        = 0 ;

        din       = 0 ;

        # 200 ;

        forever begin

            @(negedge clk) begin

                en          = 1 ;

                din         = stimulus[i] ;

                if (i == SIN_DATA_NUM-1) begin

                    i = 0 ;

                end

                else begin

                    i = i + 1 ;

                end

            end

        end

    end



    cic #(.NIN(NIN), .NMAX(NMAX), .NOUT(NOUT))

    u_cic (

     .clk         (clk),

     .rstn        (rstn),

     .en          (en),

     .din         (din),

     .valid       (valid),

     .dout        (dout));



endmodule // test

仿真结果

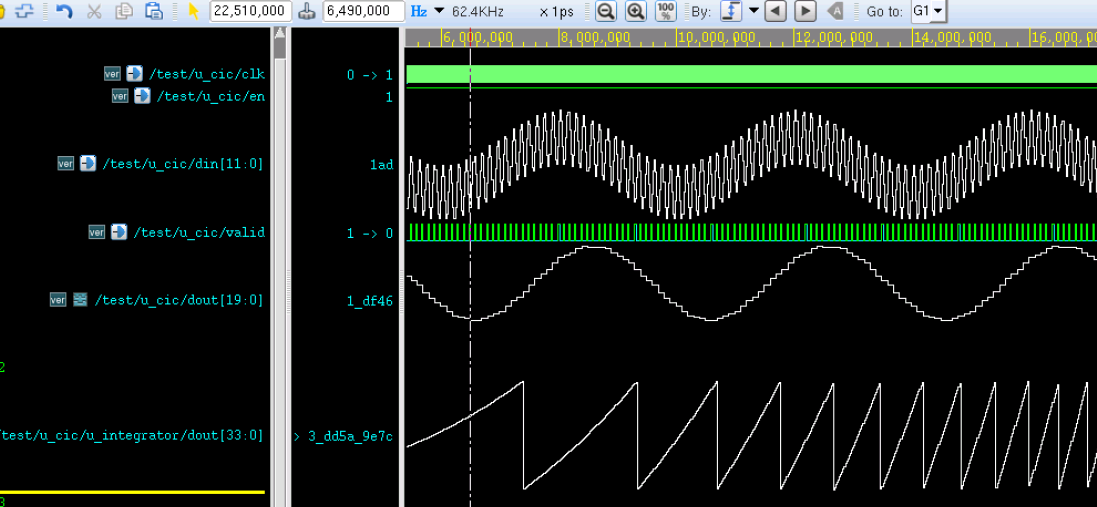
由下图仿真结果可知，经过 CIC 滤波器后的信号只有一种低频率信号（250KHz），高频信号（7.5MHz）被滤除了。

但是波形不是非常完美，这与设计的截止频率、数据不是持续输出等有一定关系。

此时发现，积分器输出的数据信号也非常的不规则，这与其位宽有关系。

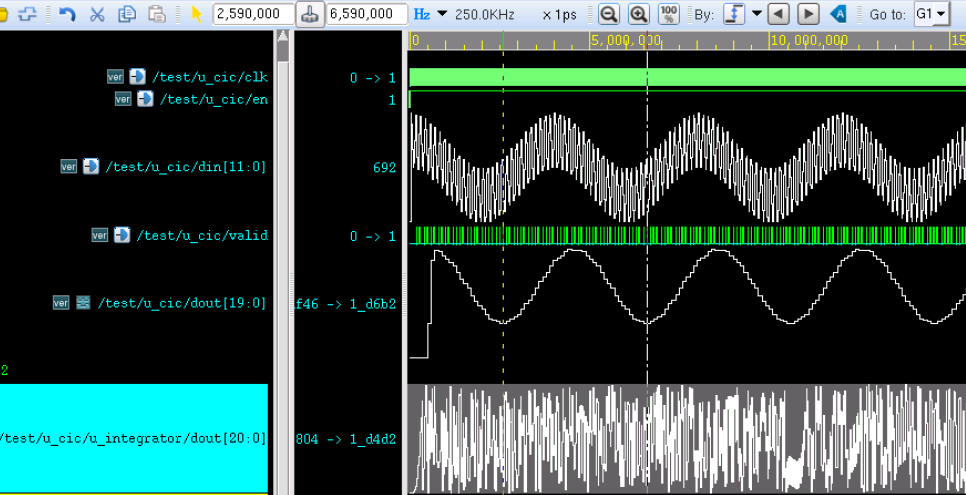
20211122192205330298621

为了更好的观察积分器输出的数据，将其位宽由 21bit 改为 34bit，仿真结果如下。

此时发现，CIC 滤波器的数据输出并没有实质性的变化，但是积分器输出的数据信号呈现锯齿状，也称之为梳状。这也是梳状滤波器名字的由来。

20211122192205590534622

源码下载

Download

计算机