SciPy 稀疏矩阵

SciPy 稀疏矩阵

稀疏矩阵（英语：sparse matrix）指的是在数值分析中绝大多数数值为零的矩阵。反之，如果大部分元素都非零，则这个矩阵是稠密的(Dense)。

在科学与工程领域中求解线性模型时经常出现大型的稀疏矩阵。

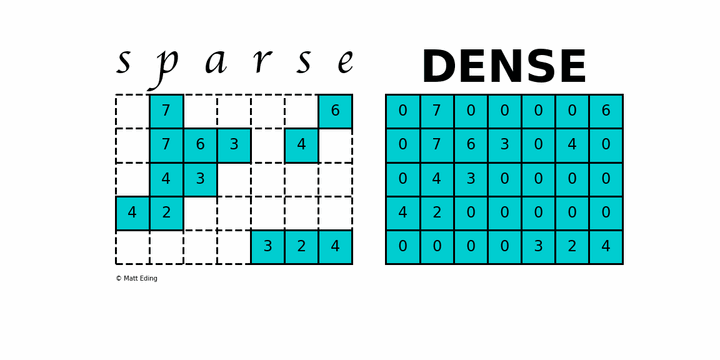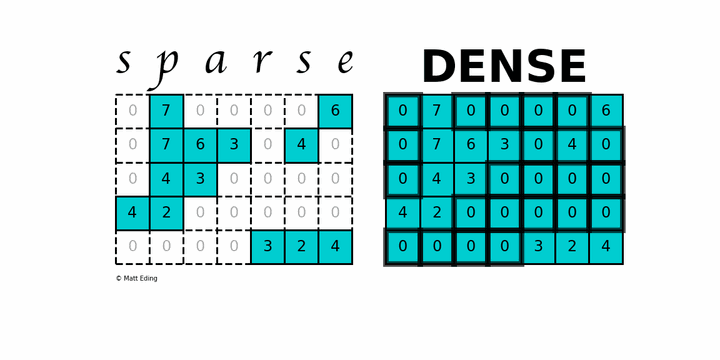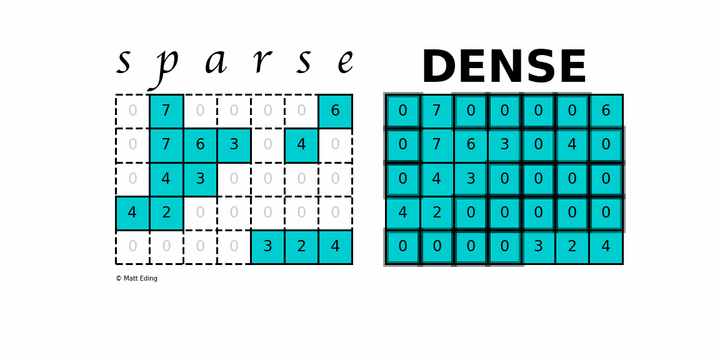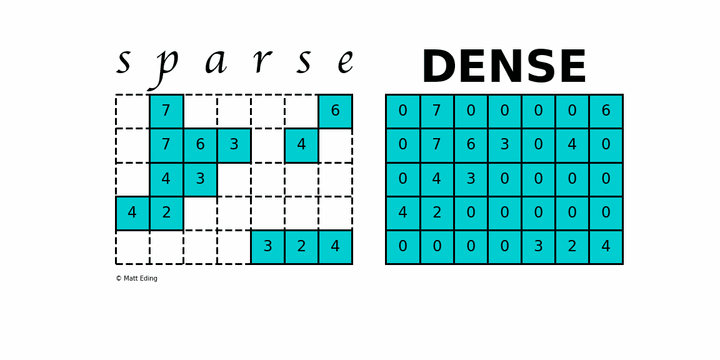
上图中左边就是一个稀疏矩阵，可以看到包含了很多 0 元素，右边是稠密的矩阵，大部分元素不是 0。

看一个简单例子：

上述稀疏矩阵仅包含 9 个非零元素，另外包含 26 个零元。其稀疏度为 74%，密度为 26%。

SciPy 的 scipy.sparse 模块提供了处理稀疏矩阵的函数。

我们主要使用以下两种类型的稀疏矩阵：

• CSC - 压缩稀疏列（Compressed Sparse Column），按列压缩。
• CSR - 压缩稀疏行（Compressed Sparse Row），按行压缩。

本章节我们主要使用 CSR 矩阵。

CSR 矩阵

我们可以通过向 scipy.sparse.csr_matrix() 函数传递数组来创建一个 CSR 矩阵。

实例

创建 CSR 矩阵。

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([0, 0, 0, 0, 0, 1, 1, 0, 2])



print(csr_matrix(arr))

以上代码输出结果为：

  (0, 5)        1
  (0, 6)        1
  (0, 8)        2

结果解析：

• 第一行：在矩阵第一行（索引值 0 ）第六（索引值 5 ）个位置有一个数值 1。
• 第二行：在矩阵第一行（索引值 0 ）第七（索引值 6 ）个位置有一个数值 1。
• 第三行：在矩阵第一行（索引值 0 ）第九（索引值 8 ）个位置有一个数值 2。

CSR 矩阵方法

我们可以使用 data 属性查看存储的数据（不含 0 元素）：

实例

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])



print(csr_matrix(arr).data)

以上代码输出结果为：

[1 1 2]

使用 count_nonzero() 方法计算非 0 元素的总数：

实例

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])



print(csr_matrix(arr).count_nonzero())

3

实例

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])



mat = csr_matrix(arr)

mat.eliminate_zeros()



print(mat)

  (1, 2)    1
  (2, 0)    1
  (2, 2)    2

使用 sum_duplicates() 方法来删除重复项:

实例

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])



mat = csr_matrix(arr)

mat.sum_duplicates()



print(mat)

  (1, 2)    1
  (2, 0)    1
  (2, 2)    2

csr 转换为 csc 使用 tocsc() 方法：

实例

import numpy as np

from scipy.sparse import csr_matrix



arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])



newarr = csr_matrix(arr).tocsc()



print(newarr)

  (2, 0)    1  (1, 2)    1  (2, 2)    2